Find the Center of the Dihedral Group D4

We can picture this through a smaller even dihedral group such as D4 shown below. You may use the fact that feˆ.

Z Dn Centre Of A Dihedral Group D4 Abstract Algebra Group Theory Youtube

What is the order of dihedral group D4.

. Let D 4. The rotations rr2r3 of 90180270 counterclockwise respectively about the center of S. We review their content and use.

Let N be a normal subgroup of D4. If n is even it contain 1 and rn2 elements. In mathematics a dihedral group is the group of symmetries of a regular polygon which includes rotations and reflectionsDihedral groups are among the simplest examples of finite groups and they play an important role in group theory geometry and chemistry.

For even n 4 the center consists of the identity element together with the 180 rotation of the polygon. The elements of D n are 1ˆˆ2ˆn 1 and ˆˆn 1. The dihedral group of order 8 D4 is the smallest example of a group that is not a T-group.

S11MTH 3175 Group Theory ProfTodorov Quiz 4 Practice Solutions Name. Ections a rotation by a multiple of 2ˇnradians around the center carries the polygon back to itself so D n contains some rotations. Although this notation is overly explicit it does help to resolve the ambiguity with the Lie type D l which corresponds to the orthogonal group Ω 2 l q.

The identity mapping e. Who are the experts. If or then is abelian and hence Now suppose By definition we have.

Listing its elements relations between rotations and re ections the center and conjugacy classes. Find the center of the Dihedral group D4. Text Prove that the quaternion group is not isomorphic to the dihedral group D_4.

Tˆt ˆ 1 be the dihedral group. 1rr2r3 d 1d2b1b2 where r is the rotation on 90 d 1d2 are flips about diagonals b1b2 are flips about the lines joining the centersof opposite sides of a square. The center of the dihedral group Dn is trivial for odd n 3.

Center of dihedral groups. Where is an element of order 2 is an element of order and are related by the relation It then follows that and in general. In this case we are looking for D4 so the number of elements in center will be 2 which is 1 and r2.

Let D4 denote the group of symmetries of a square. The join of abelian subgroups of maximum order the Thompson subgroup is the whole group dihedral groupD8 so its center is. A Calculate the centre of the dihedral group D 3 the group of sym-metries of an equilateral triangle.

Finding the elements of D n. See the answer See the answer done loading. Surjective homomorphism from the infinite dihedral group to each finite dihedral group Hot Network Questions How to fairly assess applications coming from Islamic countries for a master programme in the USEurope.

Contemporary group theorists prefer D 2 n over D n as the notation for the dihedral group of order 2 n. Find the center of D 4 the dihedral group of order8. A Write the Cayley table for D 4.

ZD10 e r5 This generalizes to ZDn e rn2 for n is even. This problem has been solved. Let D_8 be the dihedral group of order 8.

Centralizer Normalizer and Center of the Dihedral Group D_8. Abelian and any element acting quadratically on it acts linearly on it roughly speaking In a group of nilpotency class two this subgroup coincides with the center. Dihedral group D 4 1.

The center consists of the identity and r5 where r is a frac110 rotation. Let and let be the dihedral group of order Find the center of. We will look at elementary aspects of dihedral groups.

B Calculate the centre of the dihedral group D 4 the group of sym-metries of the square. We review their content and use your feedback to keep the quality high. Let SABCD be a square.

Math Advanced Math QA Library Consider a dihedral group D4 1Find all the conjugacy classes of D4. What is Centre of dihedral group. Discuss all the possible commutators of D4 and verify that 1st derived subgroup of D4 D4 1a2.

Prove that the quaternion group is not isomorphic to the dihedral group D 4. Show transcribed image text Expert Answer. Elements in the Center commute with all other.

Well look at the general case of D n for n 3. Experts are tested by Chegg as specialists in their subject area. The notation for the dihedral group differs in geometry and abstract algebraIn geometry D n or Dih n refers to the.

The center of the symmetric group Sn is trivial for n 3. See the answer See the answer See the answer done loading. Any of its two Klein four-group subgroups which are normal in D4 has as normal subgroup order-2 subgroups generated by a reflection flip in D4 but these subgroups are not normal in D4.

Give the detail of your work 2. In mathematics a dihedral group is the group of symmetries of a regular polygon including both rotations and reflections. D 4 D 4 e ˆ ˆ2 ˆ3 t tˆ tˆ2 tˆ3 e e ˆ ˆ 2ˆ3 t tˆ tˆ tˆ3.

Give the detail of your work 2. Using the generators and relations we have. D4 has 8 elements.

The various symmetry mappings of S are. Let S 0 and ˆ R 2ˇn. Find the order of D4 and list all normal subgroups in D4.

D_8langle rs mid r4s21 srr-1srangle aLet A be the subgroup of D_8 generated by r that is A1rr2r3. The dihedral group D4 is the symmetry group of the square. Tˆ3g are all distinct elements of D 4.

Who are the experts. Dihedral groups are among the simplest examples of finite groups and they play an important role in group theory geometry and chemistry. Prove that the quaternion group is not isomorphic to the dihedral group D 4.

For all integers Now since and together. The group of rotations and reflections of a regular polygon. The center of the quaternion group Q8 1 1 i i j j k k is 1 1.

D 4 stands for the group of symmetries of the square. Dihedral groups arise frequently in art and nature. Center of Dn contains only 1 if n is odd.

Dihedral group D4 synonyms Dihedral group D4 pronunciation Dihedral group D4 translation English dictionary definition of Dihedral group D4. Find the center of the Dihedral group D4. Experts are tested by Chegg as specialists in their subject area.

Solved 4 4 Consider The Dihedral Group D4 A B E A Chegg Com

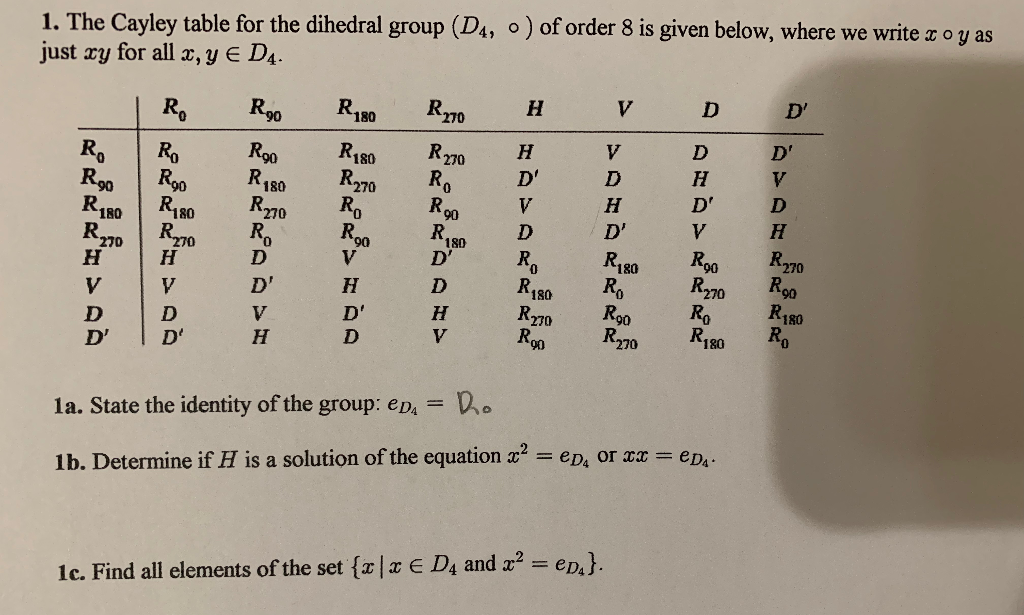
Solved 1 The Cayley Table For The Dihedral Group D4 O Of Chegg Com

Z Dn Centre Of A Dihedral Group D4 Abstract Algebra Group Theory Youtube